
***********************************
**********************************
*よりハッピーになる微笑み空間をつくりましょう!!*
・-・-・ 15の幾何学的性質 ― 良い形 ― ・-・-・
***********************************
***********************************
涼やかな風が、秋の気配を感じさせるこの頃ですが、
いかがお過ごしですか。
新しい季節、新学期を良いかたちで、スタートさせたいですね。
いつもご購読ありがとうございます。(*^o^*)
今回は「生きているプロセス」から生成される「生きている構造」に、
結果として備わる幾つかの性質、15の性質の中の
「GOOD SHAPE − 良い形」について
取り上げたいと思います。♪♪(^o^)♪♪
(The Nature of Order 1 p.179〜p.185)
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
アレグザンダー教授は、こう始めています。
「私が、生きている構造を探し始めた時に、
分析を定義するとその数だけ出来てしまうくらい、
どんなにか他の特徴と混ざり合っているかということを見出して、
驚いたのでした。時々この形の美しさは、
微妙で、複雑で、分析を超えているように見えます。
そして、良い形として考え始めた特別な質に気が付きましたが、
良い形を説明したり、定義したりする事は、
全く容易なことではないと知ったのでした。」
以下、どうぞ、下記より写真をご覧になりながら、お読み頂けたら、ハッピー!!
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
「写真のベルベット錦織上の扇形の花が、それを見せています。
ルーマニアの堂々たる木彫が、その愛すべき力強い形が、それを見せています。
日本の神社の強烈ともいえる形が、見せています。
アッバス朝の石彫上の彫られた形がシンプルに繰り返して、
力強い形が、それを見せています。
長い時間、私はただ、それらを集めて、
それらが良い形を備えているとメモしておいたのでした。
しかし、それは、どういう意味なのでしょうか。
良い形とは、何でしょうか」と。

☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
「良い形自体もセンター、中心性に関係しているということに気が付くのに、
時間が掛かりました。それは、むしろ、私達が良いとしてみる形は、
それ自体、いくつもの多様な一貫したセンター、
中心から出来上がったひとつの形なのです。
例えば、トルコのベルベット織で、
扇形の葉に見られる形の美しさは、
いくつもの多様なセンター、中心から、
それぞれ個々の形がつくられる特有な方法故に、起きているのです。(^_-)☆
その点を明確にする為に、二つの例を取り上げてみましょう。
ひとつは、それ自体とても良い形を備えていますが、
他方は、全く良い形を欠いてしまっている物です。
どうぞ、写真をご覧ください。
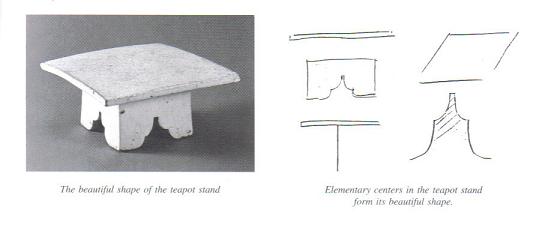
日本の茶卓は、それ自体、美しい良い形を備えています。
その形の全ての部分に中心を備えていて、
そして、それが、形を良くしているのです。
対照的に、未来志向の椅子は、はなはだしく酷い形で、
どこの部分も、中心、センターを持たずに、
それが、その形全体を悪くしてしまっているのです。

「良い形」とは何でしょうか。何がそれをつくるのでしょうか。
何度も繰り返し起こる法則として、良い形を理解するのが、最も容易です。
その繰り返し起こるという法則は、どんな良い形の要素も、
いつもそれ自体が良い形であると言える事です。
または、センター、中心という言葉を用いて、言えるでしょう。
良い形は、いくつもの力強く、強烈なほどのセンター、中心によって出来ていて、
そのセンター自体が良い形なのです。
加えて、最も単純な、最も要素として良い形は、
要素の輪郭から起きていることに、注目です。
然るに、初めに気が付くことは、良い形はほとんどの場合、
どんなに複雑であっても、
最も単純な、要素の輪郭から構成されていているということです。
茶卓は、図のように、それぞれが良い形を備えている単純な形によって、
構成されていることが見て取れます。
ひとつの構成要素の中心として、
茶卓のとがらせた唇のような足の下のポジィティブ・スペースの形をも
意味していることに注目です。
他方で、未来志向の椅子の、形の無い塊は、
シンプルな要素といえる形で構成されていると理解することが、全く出来ません。
もしも、誰かが、部分に分けて、その構成要素の形を定義しようとしても、
それらは、また再び、とても酷い形となっているのです。
結果として、それは、全くセンターを創っていません。
空間が真に全体となっている時、その要素は、ある意味で、
かなりより整然としている、系統だった形から、いつも出来上がっているのです。
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
さあ、次の写真のペルシャ絨毯を見ながら、より詳細に渡って理解し始めましょう。

それは、表面的には「花柄」に見えます。

しかし、近くで調べると、
三角や、ひし形や、六角形や、矢形や、円の一部や、
全てむしろ系統だった形を含んだ、
よりシンプルな形から出来上がっていると見て取れます。
そして、それらの系統だった形の規則性が、形の間で、
大変多くの曖昧な相互関係を許容しているのです。(^_-)☆
花や葉や蕾や、開いた花や茎の形は、全て幾何学的にシンプルな形で出来ており、
小さな部分の形として力強いのです。
花びらでさえも、本質的に、直線の輪郭を持ち、
四角形や、三角形や六角形などといった形と、色と両方で、
有機的な形の幻影を創造するための大変複雑な方法で一緒にされて、
構成されています。
どうして、それがそれ程、重要なのでしょうか。
シンプルな形の規則性が、決して緩んだ有機的な形によって達成されることのない、
形の中での、とてもより複雑な相互関係の可能性を創造することが出来る(^_-)☆と、
私は信じています。(^_-)☆
複雑なセンターのように見えるものは、
よりシンプルなセンターで出来上がっていて、
そして、そのよりシンプルなセンターも生きているのです。
つまり、結局、 こうしたよりシンプルなセンターが、
複雑なものに命を与えているのです」と述べています。
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
「よりはっきりした例をみてみましょう。図をご覧ください。
極シンプルな例ですが、
別の絨毯の縁取りオーナメント(デコレーションではない装飾)です。
やはり、花のように見えます。けれども、近寄って調べると、
色付けされた小片やそれらの間の空間の両方とも、
全くダイヤモンド形や、四角形や、三角形で出来上がっていることが解かります。
その結果としてのオーナメントは、ひとつの全体として、良い形を持っています。
良い形とは、部分に留まらず、全体を構成するひとつの姿勢で、
しかし、その全体が、このむしろシンプルな幾何学的意味において、
それら自体が全体である複数部分から出来ているときに、
良い形が起きているのです。(^_-)☆
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
全くひとつの意味で、これは明らかです。
全ての段階で、デザインの全ての目にすることが出来る部分が、
良い姿形あるいは強い「実体」になるに違いない法則を適用してみましょう。
これは、明らかに、無形の斑点や、あいまいな形などを排除しますが、
四角形や、八角形や、八片の花びらの形や、
45度の二角を持つ三角形などは含んでいることは明白です。
けれども、私達が、より深くこの問題を掘り下げようとして、
形の良さを持つものを見分ける正確な法則を与えようとする時、
その考えを正しく定義することが難しくなるのです。
下記のリストは、良い形をつくるためにと、
良い形をつくる要素のために要される特徴のリストの一部分です。
1 高度な内部的対称性。
2 左右あるいは上下対象性(ほとんど、常に)。
3 ひとつの良くわかるセンター(図心である必要はありません)。
4 それがつくる隣接した空間もポジィティブ・スペース。
5 その周囲との区別が大変明らかであること。
6 相対的にコンパクトであること(その縦横の比率が1:4やそれを超えることはなく、1:1や1:2やその間の輪郭)。
7 閉鎖的で完結している感じであること。
良い形を創っていく経験の全てにおいて、
以下の要素が最も共通しているものです。
四角形、棒形、矢先形、鉤形、三角形、点の列、円、薔薇形、ダイヤモンド形、
S形、半円形、星形、段々形、十字形、波形、らせん形、樹木形と八角形です。
私達が、「良い形」として認めるものは、ただ、最も強く中心、センターをつくっているそれらの複合したものなのです。
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
私達がそれを適用しようとした時、これは、全く微妙です。
たとえば、円形をとってみましょう。
対称性のあるコンパクトな形ですで、良い形として現れます。
または、誰かがそのように主張します。
しかし、円形には、大きな問題があります。
それは、隣接する空間をポジィティブすることが、容易ではないということです。
更に、デザインするときに円を用いると、
それを良い形にするのは全く容易ではないのです。
このような例として、コペンハーゲン警察本署の建物をご覧ください。
途方も無いプランで、円形の隣接した空間が無形で、
それで無意味となってしまって、つまらないものとなっています。
かなり高度の洗練が、円形を良い形にするには必要で、
例えば、それは、写真の驚くほどに素晴らしいオットーマン・ベルベット織に見られます。
そこに描かれている2つの円形は、僅かに歪んでいて、(^_-)☆
それで、月形も、円の間の空間も、大きな円も小さな円も全て、
中心、センターとして働いているのです。
そのパターンは、その力強さゆえ、肝をつぶす程です。
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
結局、良い形の質は、ひとつの全体としてのその形自体が、
力強く素晴らしくなる時、ざっと説明したような良い形を備えたときだけ生じるのです。
写真の古代ギリシャの馬頭彫刻、初期のキリスト教会のプランなど、
それらは全て、極度ともなるような大きく、素晴らしい感覚の中で、
良い形を見せています。
特に、丸っぽい目を持った馬のは、
3次元の生きている中心、センターから刻まれている忘れ難い形を創造しているのです。
そして初期のキリスト教会のプランは、
ほとんど反対で、驚くほど、単純で、静か…..ですが、
同じ方法で、構成されていますので、
単純な要素が一緒に、忘れ難い形を創り上げているのです。
どんなにか境界東端奥室と多くの四角形が一緒に、
その構成の中で部分的に対称性を形成しながら、
全てを創造しているか、全ての何か、事実として、シンプルで、
しかし、忘れ難いのです。古代の心につきまとう旋律のように。

そして、おそらく全ての中で最も美しい例ですが、
エジプトの帆船の愛すべき航海の姿が、
驚くほどの度合いの良い形の質を備えています。
私達は、直ぐにそれを見て感じ取り、
それが持つ強烈で愛すべき特徴を感じるのです。
しかし、分析してみると、
航海中のひとつひとつの帆の形が、
控えめで、優しくカーブしていて、それ自体がセンターで、
そして、それらから、この複雑な形が出来上がっているのです。
良い形を持つことによって、
センター、中心の命が創造されるのです。(^_-)☆
この航海の姿は、
その幾何学的形が、沢山の良い形で創られている故に、
生きているのです。」(^_-)☆
☆★☆★☆★☆★☆★☆★☆☆★☆★☆★☆★☆★☆★☆☆★☆
その航海の姿が生きているということは、
美しいだけではなくて、風と調和して、帆船がその意味たる働きを、
愉しくなるほど、全うしている姿とも見て取れますね。
それで同時に、命の光を発するような美を、私達に見せてくれています。(*^o^*)
ひとつひとつの部分がセンターをもち、単純な良い形をもち、
そして複雑な良い形、全体が命を持つようになるということは、
全ての実体、建築、まち、法律の条文にさえも言えることではないでしょうか。
あの良い形をつくるための、良い形をつくる要素の7項目を思い出して見ましょう。
個々の条文が、緩みが無く完結して、良い形で、
全体に貢献する姿勢をもって、そして、
それらで創り上げる全体が、複雑でも良い形になるのではないでしょうか
その法律の存在意義を全うするように、
個々の条文に緩みとなる多くの例外を付けることなく、
其の上で、全体の中で、成長する方向付けをしておくのです。
公共建物の中庭は、公共広場は、沢山の箇所から通り抜けられるのではなく、
調度、私達の胃袋の形ように、筒抜けではない、抜けがあるのが良い形のようです。
法律も、皹や緩みではなくて、その抜けていく方向、
成長していく方向付けをあらかじめ設定しておくと、
樹木のように良い形になるのではないでしょうか。(*^o^*)
私の暮らす練馬区で、念願の「まちづくり条例」が策定過程にきているので、
気になるところでして、これで、多くの人が、
ただ住んでいるだけの住民から、
地域社会を担う市民へのスタートが良い形で切れたら、ハッピー!!
次回は、「LOCAL SYMMETERIES」です。♪♪(^o^)♪♪
どうぞ、お楽しみに(∩o∩)ノ
リンク: http://www.smilingspace.com
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
このメールマガジンは、『まぐまぐ』 http://www.mag2.com/ を利用して発行
しています。登録・解除は http://www.mag2.com/m/0000090643.htm
からできます。
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−